ナップサック問題に対する分枝限定法 P 0 1 b z c x n n j j j 制約条件 : 目的関数 最大 ≤ = → ∑ ∑ = を仮定する。 与えられた正整数 a b a c b n j j j ∑ > 0,1, 1,2, , 1 x j n a x b j j j j ・・・ 制約条件 = = ∑ ≤ = j=1 :品物 の重さナップサック DP は、$n$ 個の対象それぞれに対して「選ぶ」「選ばない」の2通りの選択肢を考えていく過程を効率よく実現できる手法でした。 今回はこれを利用して、下図のような「連続する $n$ 個のアイテムを各区間に最適に分割する問題」を考えてみましょう。;n) ナップサック問題の解は変数の整数条件を外した 線形最適化問題の解とは一般には一致しない 欲張り法も最適解が得られる保証はない

B 2 3 分枝限定法
分枝限定法 ナップサック c++
分枝限定法 ナップサック c++-分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 巡回セールスマン問題:次に訪問する都市によって場合分けナップサック問題(ナップサックもんだい、Knapsack problem)は、計算複雑性理論における計算の難しさの議論の対象となる問題の一つで、「容量 C のナップサックが一つと、n 種類の品物(各々、価値 p i, 容積 c i )が与えられたとき、ナップサックの容量 C を超えない範囲でいくつかの品物を



Approximation Algorithms For Combinatorial Optimization Problems Speaker Deck
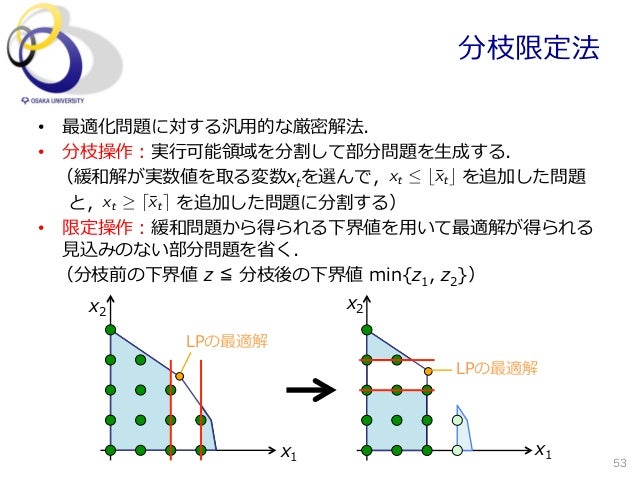
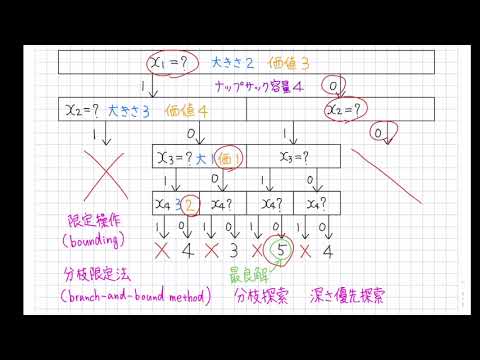
分枝限定法 巡回セールスマンやナップサック問題のような組み合わせ最適化問題を解くことを考える。解の組み合 わせは有限なので、すべての組み合わせを列挙して評価すれば最適解が得られるが、組み合わせの数は 膨大であり効率が悪い。分枝限定法 分岐限定法は、分岐操作と限定操作から成ります。 分岐操作とは、場合分けによって問題を、部分問題に分割する操作を指します。 例えば、重量制限が4kgのナップサック問題の場合、解法 分枝限定法(Branch and Bound) まず始めに01 ナップサック問題 を整数計画問題として定式化します. 変数 xi は値が 1 のとき i 番目のアイテムを選択し, 0 のとき選択をしないことに対応しています. 分枝限定法は変数の値を順番に0か1かに固定していき分枝木を探索していきます.探索の途中で変数 xi の値を決めるときに, x1, x2, , xi − 1 の値はは 0 または 1
分枝限定法の実装 基本的な分枝限定法として01 ンプルな理解のために発見的な手法による工夫を効率順でのソーティングにしぼったナップサック問題に対する分枝限定法を実装した 今回はよりシ 31 01 基本的な実装 ナヅブサヅク問題は,分枝限定法 分枝カット法 動的計画法 ... 近似解法最適解を求めることを諦めて,ある程度最適値に近い値をもつ実 行可能解をなるべく早く求める 制度保証付き近似解法 メタヒューリスティック(タブーサーチ,遺伝的アルゴリズ ム,アニーリング法次のナップサック問題を分枝限定法により解け。 (問題 KP0 )max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的計画
分枝限定法 ナップサック問題 最大化z = ∑n i=1 cixi 制約条件 ∑n i=1 aixi b xi 2f0;1g (i = 1;2;分枝限定法データ構造 • 初期値g=∞,z=∞ –a{p0},n{p0},o=φ – x0={#,#,#,#, g, z} • 節点0 –aリスト{p0}分枝限定法(ぶんしげんていほう、英 branch and bound, BB )は、各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。 分枝操作(英 branching operation )と限定操作(英 bounding operation )から構成される。 全ての解候補を体系的に列挙するもので、最適化さ



B 2 3 分枝限定法



組合せ最適化入門 線形計画から整数計画まで
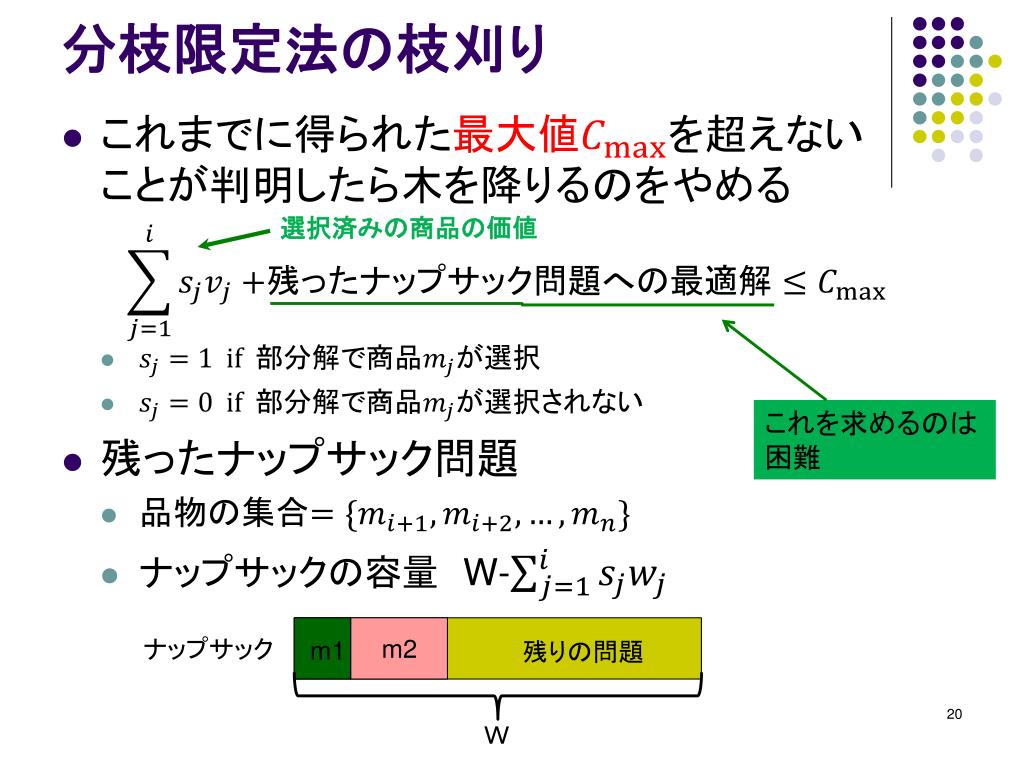
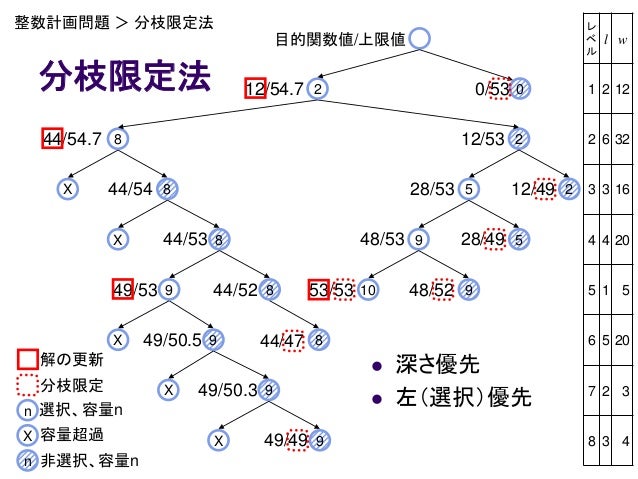
ナップザック問題(分枝限定法) 目的 ナップザック問題とは、 「$n$個の荷物がありそれぞれ($i=1,2,,n$)に価値$v_i$と重さ図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元の動的計画法 この問題の解法として動的計画法という方法があります。 ナップザックの容積以下の全ての値を最大容積としたとき、それぞれの最大容積に対して品物の種類を増やしながら最大価値を求めていきます。 サンプルコード 以下がサンプルコード


7 3 分枝限定法の並列化の利用



1995 号 最適解探索方式および最適解探索方法 Astamuse
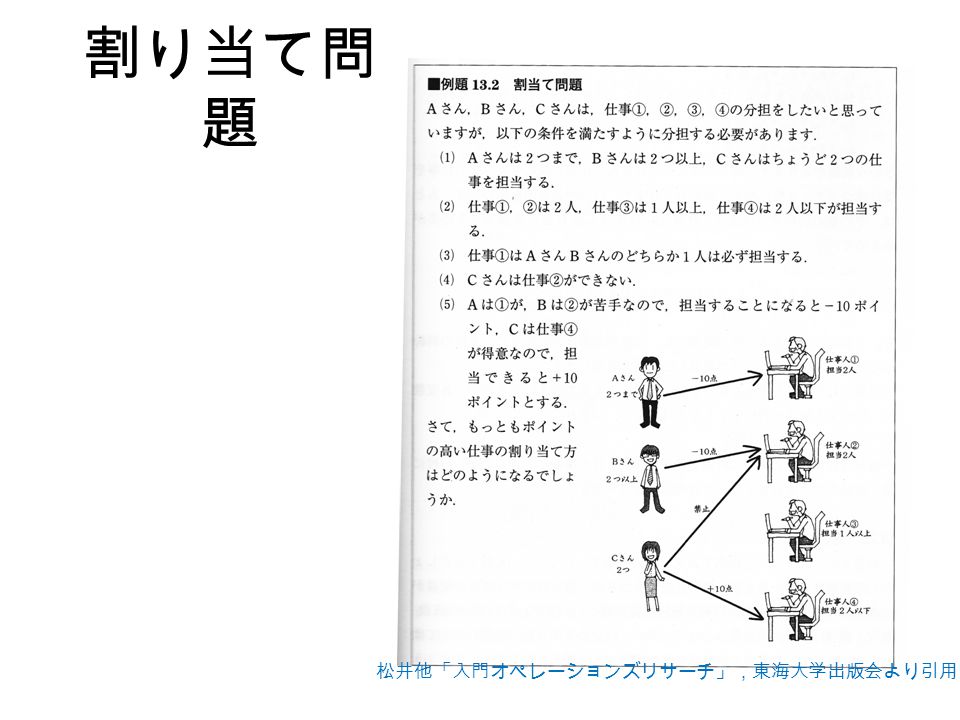
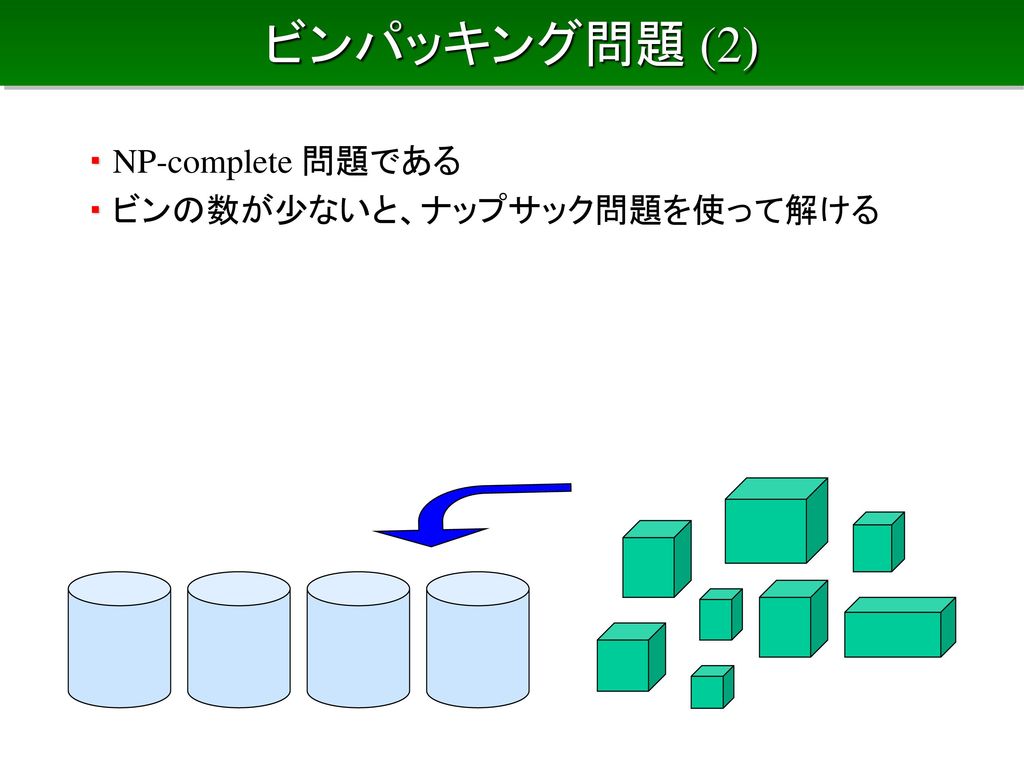
容量Cのリュックサック(入れ物)に物を入れていきます。 その時にW(重さ)がC(容量)を超えないように組み合わせて入れていく必要があります。 そうしたときに最もV(価値)が高くなる組み合わせを選ぶというものです。 今回ですと、容量10のナップサックに以下の4つのものを組み合わせて入れていきます。 番号0 W = 4 V = 32 番号1 W = 7 V = 35 番号2 W = 6 V = 24分枝限定法 分枝カット法 動的計画法 ... 近似解法最適解を求めることを諦めて,ある程度最適値に近い値をもつ実 行可能解をなるべく早く求める 制度保証付き近似解法 メタヒューリスティック(タブーサーチ,遺伝的アルゴリズ ム,アニーリング法分枝限定法 帰着とnp完全性 分枝限定法 上界と下界による限定操作 ナップサック問題 ナップサック問題 (2) ビンパッキング問題 ビンパッキング問題 (2) 巡回セールスマン問題 問題の難度と解法 01整数計画として定式化 ハミルトンサイクルが解ける 問題の
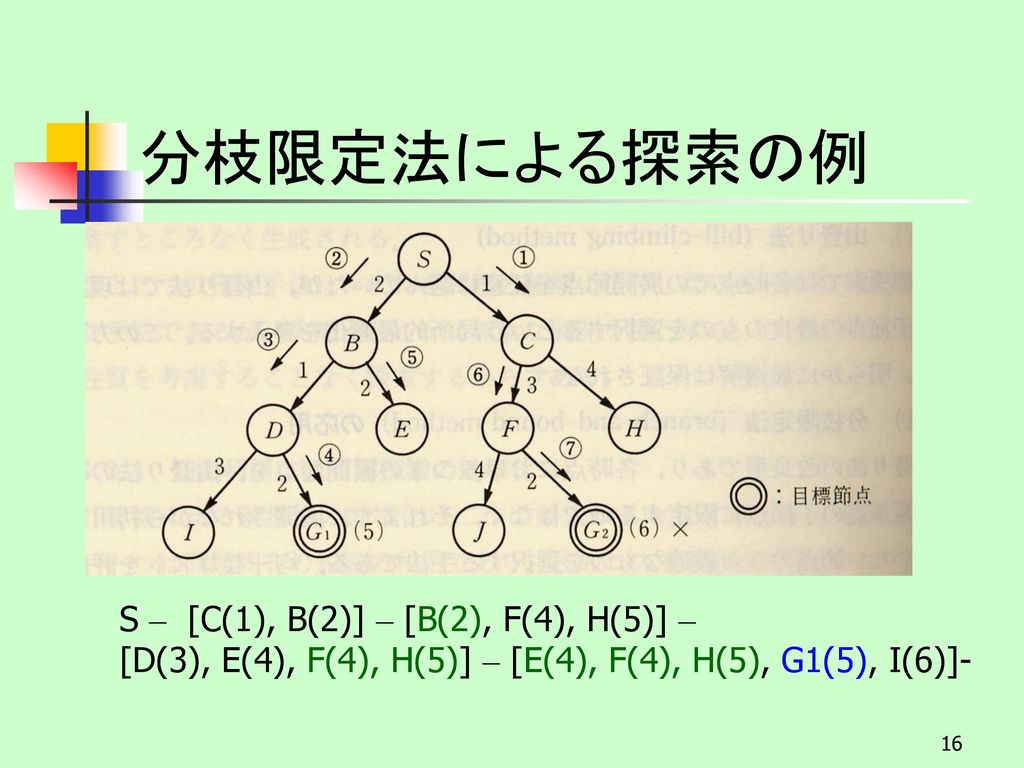


第8回 問題解決 Ppt Download


7 3 分枝限定法の並列化の利用
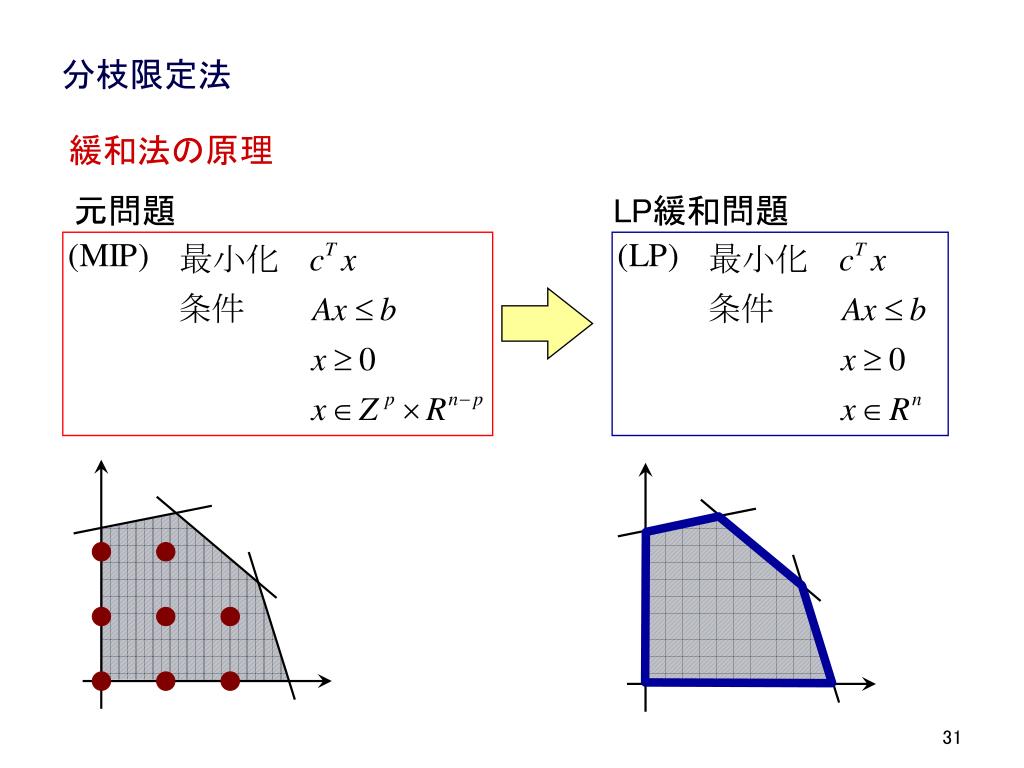
線形計画法 数理計画法の問題の中で,評価関数や条件式が全て 変数の一次式であるものを、線形計画問題という。 線形計画法は、特徴ベクトルを とすると、次のように表せる。 (, , , ) 12 tn x =∈xx x R" n n 最小化fpxx =∑ 線形計画法 P 1 jj j= n 1 iijji 1,2, , j gaxbi k分枝限定法の手順(9)部分問題が全て終端し、チェックすべき部分問題が無い ・原問題から派生した部分問題が全て終端した。 ・従って、このときの暫定解( )0,1,1,0 7と暫定解 が最適解である。そこで探索の方法を工夫する手段として、一般に動的計画法や分枝限定法な どが用いられます。ここでは、最適解を求める代わりに、乱数を使って比較 的優良な解を求めることを考えます。 c による数値計算とシュミレーション 小高 知宏 オーム社 より



Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
ナップサック問題に対する分枝限定法 P 0 1 b z c x n n j j j 制約条件 : 目的関数 最大 ≤ = → ∑ ∑ = を仮定する。 与えられた正整数 a b a c b n j j j ∑ > 0,1, 1,2, , 1 x j n a x b j j j j ・・・ 制約条件 = = ∑ ≤ = j=1 :品物 の重さ動的計画法 この問題の解法として動的計画法という方法があります。 ナップザックの容積以下の全ての値を最大容積としたとき、それぞれの最大容積に対して品物の種類を増やしながら最大価値を求めていきます。 サンプルコード 以下がサンプルコード切除平面法,分枝限定法 分枝カット法 解きやすさ (理論的) (実際的) easy (P) hard (NP) 大規模問題も解ける 解ける問題規模が拡大中 1947年 単体法(Dantzig) 1957~60年 分枝限定法(MarkowitzManne, Eastman, LandDoig) 切除平面法(Gomory) 「はじめよう」 の理由


コストのついたグラフの探索 分枝限定法 A アルゴリズム Ppt Download



分枝限定法 ヤマカサの競技プログラミング
ナップサック問題の分枝限定法likeな最適化操作をJuMPを使って動作確認する 21/2/19 9 min 読了の目安( 約00字 ) TECH 技術記事算法を分枝限定法 4,6,9,12 に取り入れたところ, 辺密度の高い問題例に対しては既存のアルゴリズム より高速に最適解を計算できることが確認できた. 2 辺制約による定式化とクリーク 制約による定式化 本節では,排他制約付きナップサック問題の2 つバックトラック法 (backtracking)あるいは後戻り法とは,問題の解を見つけるために, 解の候補をすべて調べることを組織的にかつ効率よく行うための技法である。 難しい組み合わせ的な問題を解くための技法であり,応用範囲も広い。ここでは、その典型である、Nクイーン問題(8クイーン問題



1995 号 最適解探索方式および最適解探索方法 Astamuse



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
次のナップサック問題を分枝限定法により解け。 (問題 KP0 )max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的計画– 分枝限定法では,終端条件を満たしたときは追加を行わない • 手続きの非一義性:頂点を一つ取り出すデータ構造依存 – スタック:深さ優先探索、キュー:幅優先探索 (Ref 杉原厚吉 "データ構造とアルゴリズム", 共立出版) スタック(Stack)



動的計画法 ナップサック問題 アルゴリズム講習会
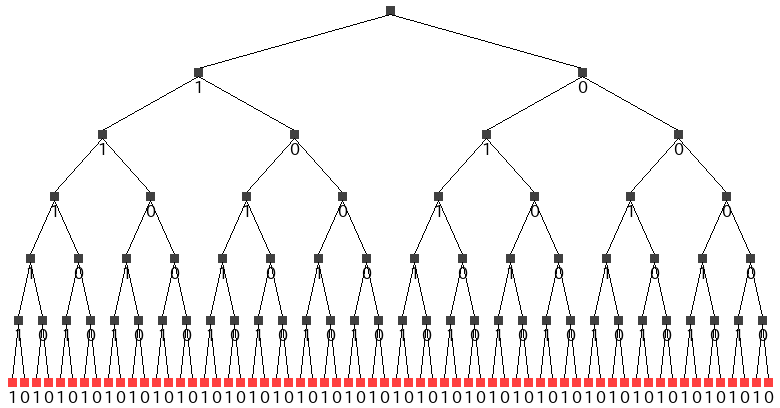


図で見る分枝限定法 Qiita



7 3 分枝限定法の並列化の利用



0 1 ナップザック問題について 2 T Nakaの阿房ブログ



組合せ最適化



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



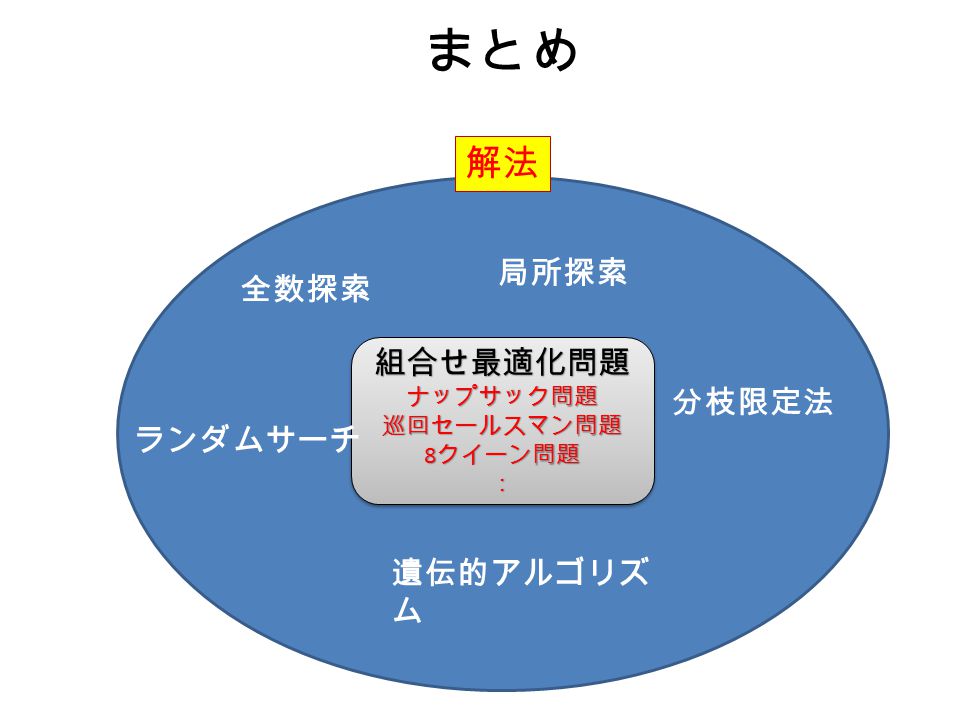
知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
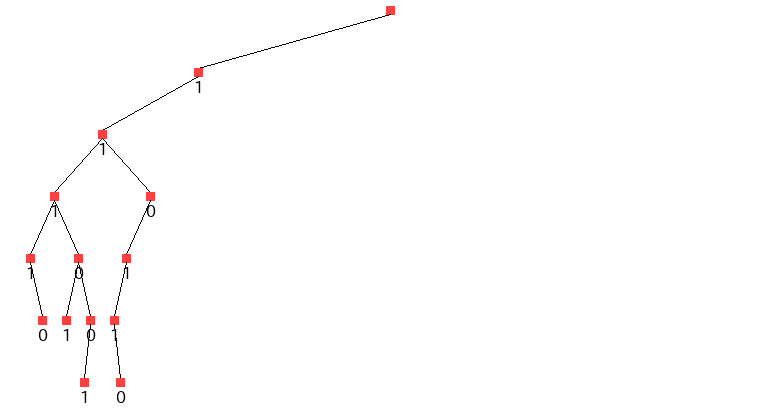


図で見る分枝限定法 Qiita



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



混合整数線形計画法 Mip アルゴリズム 入門


第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



1995 号 最適解探索方式および最適解探索方法 Astamuse


知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



組合せ最適化入門 線形計画から整数計画まで



組合せ最適化



ナップサック問題に対する分枝限定法 Youtube


Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id


組合せ最適化入門 線形計画から整数計画まで


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



ソフトウェアii 第4回 12 10 ソフトウェアii



知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



B 2 3 分枝限定法



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube



Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita



図で見る分枝限定法 Qiita


知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download
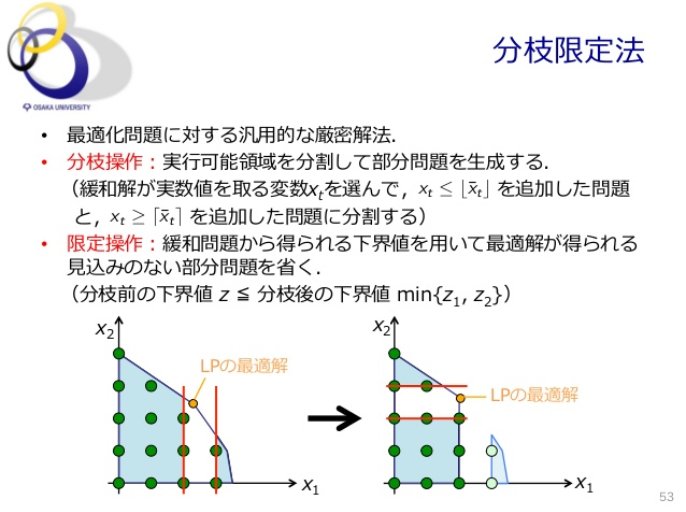


Y S R ら ぶ ぱ ぴ 完 走 し ま し た アルペで分かる 整数計画法5 伊400 だが手がないわけではない Ip問題に有効な手段の一つとして 分枝限定法がある 伊402 困難は分割せよ 分枝 限定操作によって 最適解の範囲を順次狭めていくこと



組合せ最適化



組合せ最適化



Atcoder Educational Dp Contest D Knapsack 1 ヤマカサの競技プログラミング



Operations Research Yonezawa No2



Approximation Algorithms For Combinatorial Optimization Problems Speaker Deck



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
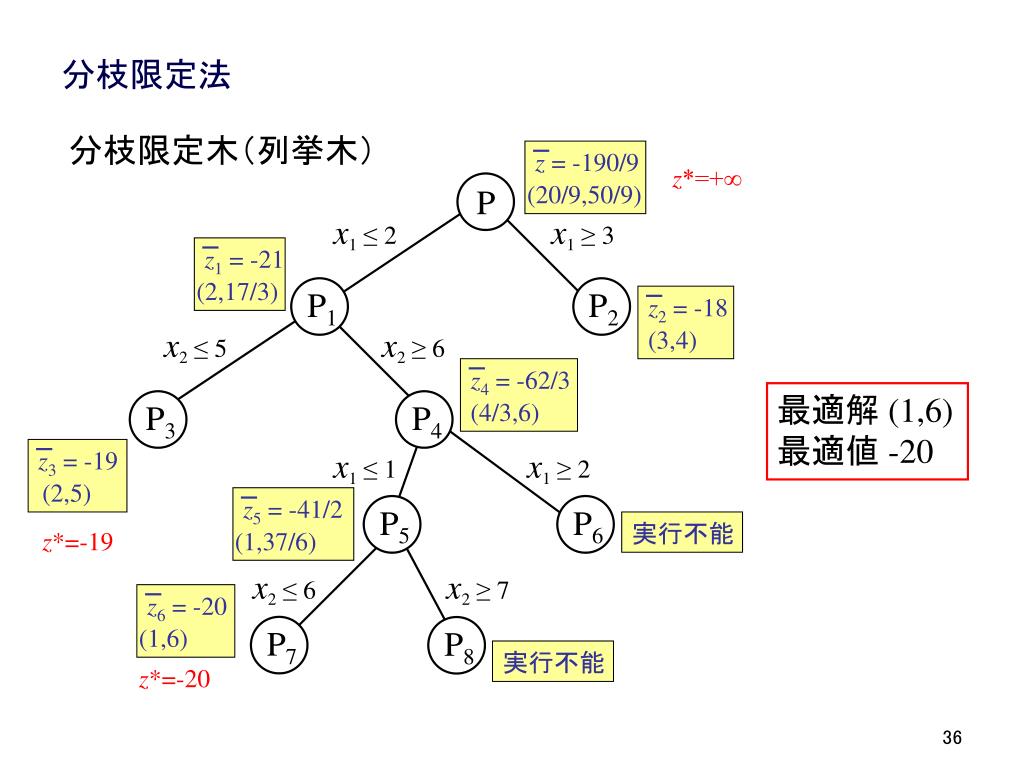


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
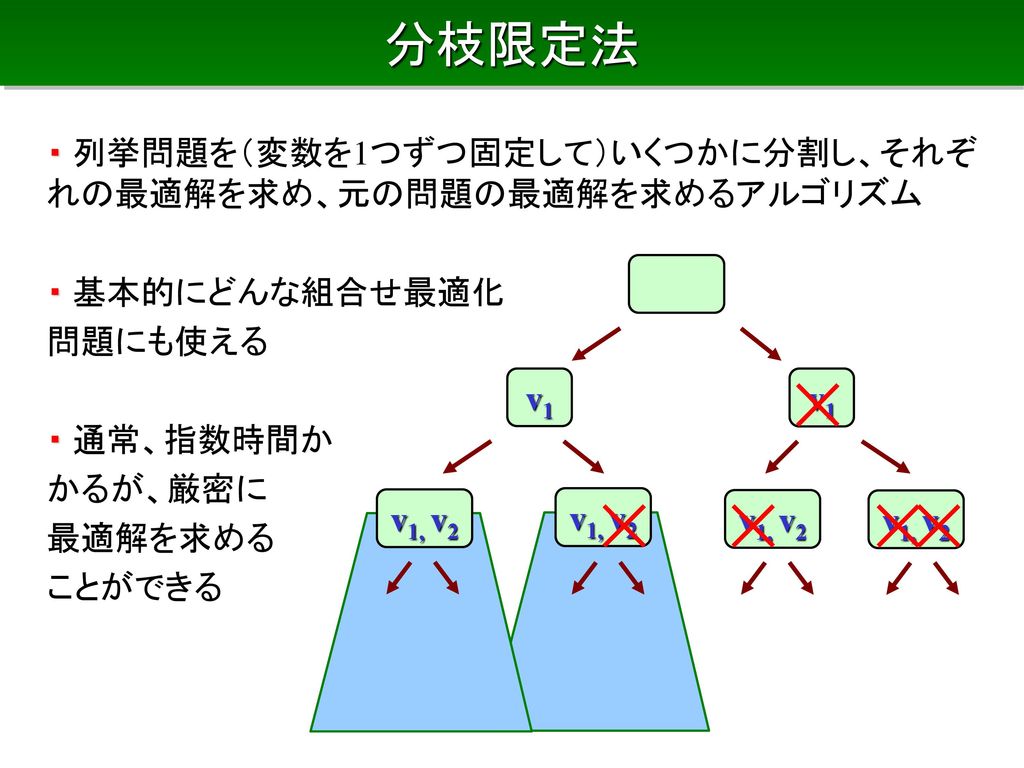


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube



コストのついたグラフの探索 分枝限定法 A アルゴリズム Ppt Download



組合せ最適化


コストのついたグラフの探索 分枝限定法 A アルゴリズム Ppt Download


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
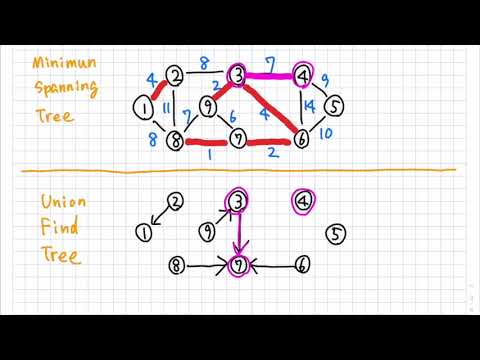


情報工学概論 アルゴリズムとデータ構造 11貪欲アルゴリズム03kruscal Youtube



ナップサック問題の分枝限定法 Likeな最適化操作をjumpを使って動作確認する


ナップサック問題に対する分枝限定法 Youtube



組合せ最適化



Efficient Algorithms For Combinatorial Optimization Problems Speaker Deck



Mathematical Optimization In 60 Minutes Speaker Deck



1995 号 最適解探索方式および最適解探索方法 Astamuse


Operations Research Yonezawa No2
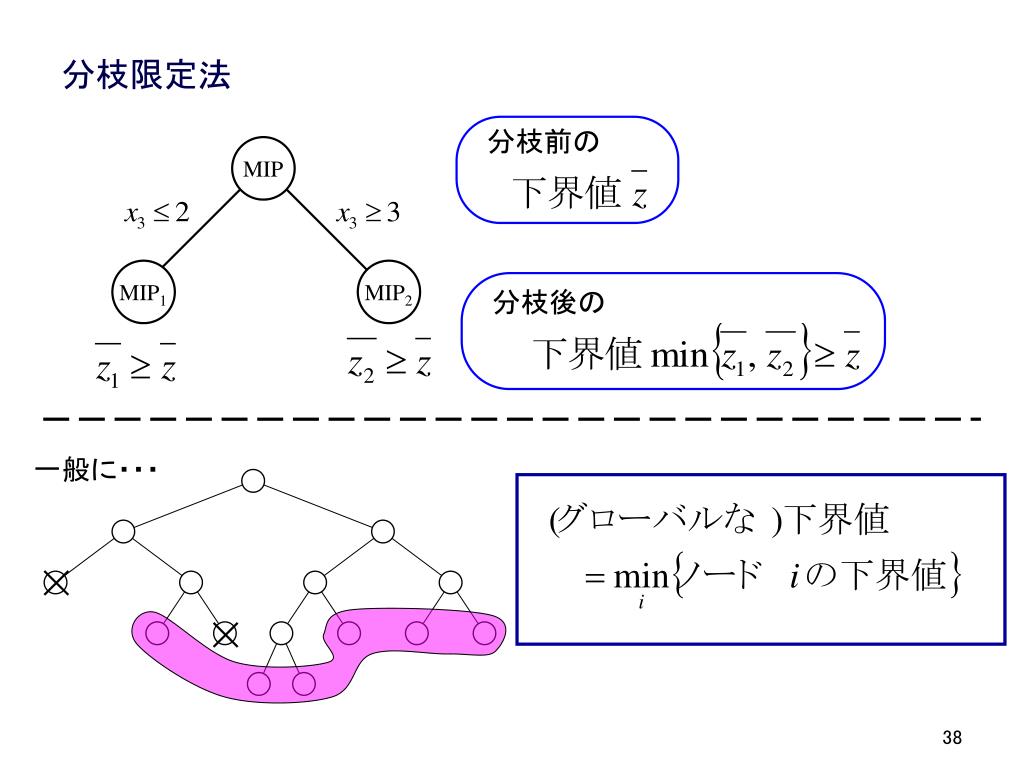


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
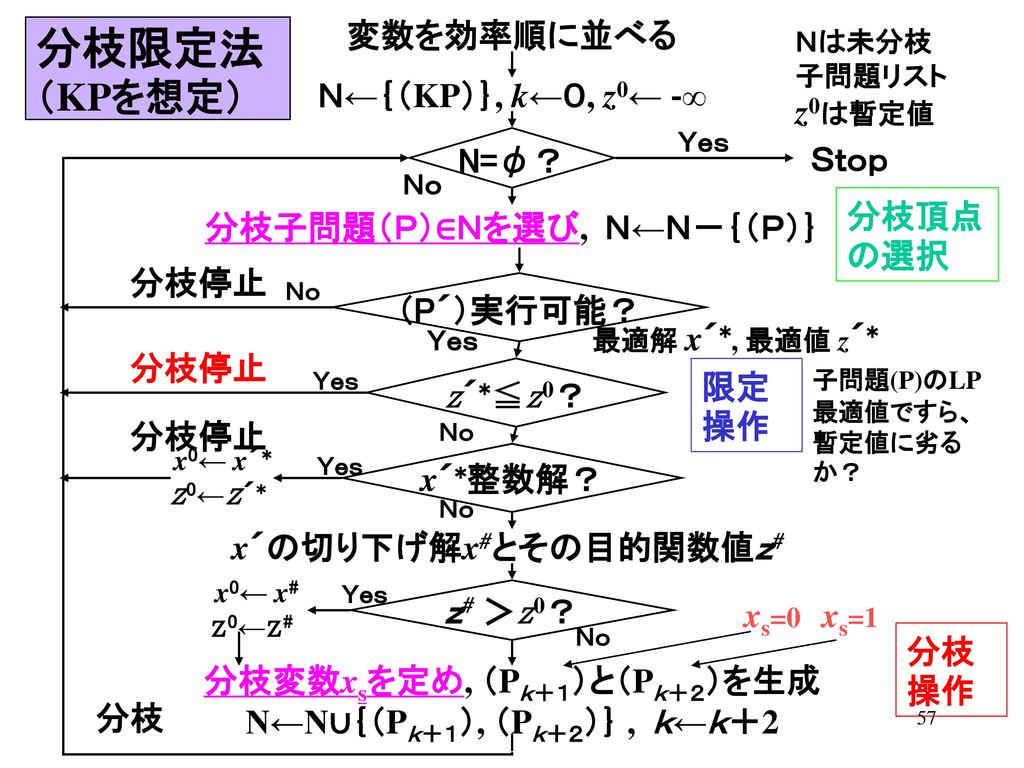


基礎or or演習 第6回 11 17 09 森戸担当分中間試験 来週 11 24 火 13 00は試験 Ppt Download



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



組合せ最適化



0 件のコメント:
コメントを投稿